1) 강의 복습 내용
Generative model은 내가 가장 관심있는 인공지능 분야다.
그리고 가장 이해하기 어려운 분야기도 하다.
특히나 수학적으로 접근해서 이해를 도출하기가 굉장히 힘든데
그 이유는 단순한 형태의 확률밀도에 대한 추론이 아니라
우도와 같이 여러 확률밀도가 동시에 발생하는 복잡한 확률에 대한 추론이기 때문이다.
likelihood 조차 이해하고 받아들이는데 얼마나 오래 걸렸는지 모르겠다.
Generative model도 오랜 시간이 걸리겠지만 꾸준히 접근해 보려 한다.
Generative model을 이해하기 위하여 간단한 Gan으로 사람얼굴을 만든다고 하자.
눈은 대칭되게 존재할 것이며
코는 눈 사이 아래에 있고
입은 코 아래에 있고
그 아래에 턱이 있고..
이런 식으로 서로의 위치가 서로의 위치에 영향을 주는가 하면
이미지의 왼쪽아래 귀퉁이는 어두워야 하고
오른쪽 아래 귀퉁이도 어두워야 하는데
머리 부분도 검게 나와야 한다.
이런 부분들은 공통점이 있어 보여도 서로 영향을 주지 않는 영역들이다.
그러면 대체 어떤 픽셀이 어떤 픽셀과 연관이 있으면 유의미한 형상이 되는 것일까.
또 어떤 연관성이 사람 얼굴, 손 글씨 등의 이미지 차이를 만들어내는 걸까.
이러한 관점을 확률론으로 풀어보도록 하자.
검정색과 하얀색 만으로 MNIST 손글씨를 만든다고 하면

이런 식의 좀 더 선명한 숫자를 얻을 수 있을 것이고
그때 28x28 이미지 한장은 n이 28*28 일때

의 확률 분포를 따르는 어떤 sample 이 된다.
즉 저런 확률분포에서 아무거나 하나 샘플링 한 경우라고 볼 수 있는 것이다.
다시 말해 저렇게 아주 복잡한 주사위를 하나 던진 것이다.
0과 1만으로 그림을 그린다고 하면 경우의 수는 $2^n$개가 될 것이다.
그러면 확률분포를 만들때 필요한 모수의 수는 몇개가 될까
첫번째 가정해볼 수 있는 것은 모든 픽셀이 서로서로 영향을 준다는 것이다.
하나의 픽셀이 0인지 1인지 알게되면 다른 픽셀도 연달아서 어떻게 될 것인가를 알 수 있을때
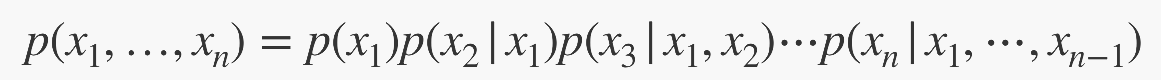
최종적으로 확률은 이렇게 표현이 될 것이고 결국 필요한 모수의 수는 $2^{n} - 1$ 이 된다.
우리는 이정도 복잡한 모수를 추론할 수 만 있으면 손글씨를 계속해서 만들어낼 수 있다.
두번째 해볼 수 있는 가정은 모든 픽셀이 서로 아무런 영향을 주지 않는다는 것이다.
이런 경우 대부분의 이미지는 salt-and-pepper 잡음처럼 보일 것이다.
하지만 아주 아주 아주 아주 드문 경우로 어떤 숫자가 나올 수 있다는 사실을 우리는 알고 있다.
그러면 이 경우는

이렇게 독립된 확률분포의 곱으로 표현되고 이 확률의 최종적인 모수는 $n$개가 필요하다고 할 수 있다.
우리는 이런 적은 수의 모수로도 손글씨를 만들 수 있다.
그렇다. 둘다 말도 안되는 이야기다.
첫번째 가정은 너무 자세하게 생각하고 있고
두번째 생각은 너무 대충대충 생각하고 있다.
그러니까 우리는 현실적으로 봤을때
서로 연관이 있는 픽셀들을 찾아서 얼마만큼 연관이 있는지 알아내고
서로 독립적인 픽셀들은 독립된 확률분포를 가지도록
첫번째와 두번째의 중간에 어디 적절하게 엮여있는 확률분포를 찾아내야한다.
그리고 그렇게 찾아낸 분포가 Generative modeling이라고 할 수 있을 것이다.
조금 더 수학적으로 말해보자.
굉장히 많은 확률변수에 의해 결정되는 joint probability는 아래의 식들로 풀어볼 수 있다.

모두 눈에 익은 식들이다. AI Math 수업을 들으면서 봤던 식들이다.
맨 아래 식은 처음 볼 수도 있는데 ㅗ 기호는 '수직' 이라고 알고 있으면 잘 알고 있는 것이다.
orthogonality 를 나타내는 기호인데 쉽게 말해 서로 수학적으로 아무런 상관이 없을 때 저 기호를 쓴다.
즉 $z$ 가 주어진 상태에서 $x$ 와 $y$ 가 서로 독립이면 conditial probability로 표현했을때
$y$가 있으나 없으나 똑같다는 의미다. 직관적으로 받아들일 수 있다.
그러면 이제 chain rule을 이용해서 모든 픽셀이 연관있는 가장 자세한 표현을 먼저 생각한 다음
어떤 $x_i$와 어떤 $x_j$ 가 서로 independent 하다고 하면 chain rule에 의해서 표현된
conditional probability 가 일부 끊어진다고 볼 수 있다.
모두가 독립인 경우 모수가 가장 적게 필요하므로
이렇게 끊어진 고리를 찾을 수록 더 적은 모수를 추정해도 된다.
또 고려하지 않아도 되는 관계들을 버림으로써 우리가 원하는 '숫자' 라던가 '얼굴' 과 같은
특정한 이미지의 분포에 더 가까워진다고 볼 수 있다.
이렇게 데이터 포인트 간의 연관성을 추론하여서 전체적인 likelihood를 찾아가는 모델을
Auto-regressive Model이라고 한다.

Auto-regresive model의 대표적인 모델로 NADE 를 꼽아주셨는데
보는 바와 같이 확률을 추론할때 점점 입력되는 픽셀이 누적된다.
그만큼 이전의 픽셀에 대한 확률 추론을 하겠다는 의미로 chain rule을 통해 나타내면 다음과 같다.

간결하게 표현이 되었다. 논문의 링크도 달아두겠다.
https://arxiv.org/pdf/1605.02226.pdf
2016년 논문으로 의외로 얼마 안된 논문이고 심지어 GAN 보다 더 늦게 나온 논문인데
수학적으로 정확히 접근하고 Image generation을 data sampling 관점에서 잘 이해할 수 있는 접근이라
정말 좋은 논문인것 같다.
위에 체인 룰을 보면 이런 생각이 딱 떠오른다.
엥 저거 완전 RNN 아니냐?


아니나 다를까 역시 관련 논문이 있다.
이 부분은 일단 패스. 뒷 내용이 또 있고 더 중요하다.
//여기부터는 내 주관적 해석이 위의 부분보다 훨씬 더 들어가 있으며
강의의 내용보다 혼자서 공부한 내용이 더 많으므로 글을 읽을때 참고하여 비판적 수용을 하길 바람.
AutoEncoder는 일반적으로 어떤 데이터셋의 latent space를 잘 찾아내고
데이터를 mapping 할 수 있는 manifold를 찾는 모델로 많이 쓴다.
그러면 고차원에서 해석하기 힘든 데이터를 저차원 manifold에서 해석하여 구분하거나
manifold에 mapping이 잘 되는 데이터인지 아닌지를 보고 anomaly 를 찾아내는 용도로 사용한다.
그러면 manifold의 중간지점을 찍어서 발견하지 못한 데이터를 추론하는 것도 가능하지 않을까?
그걸 해주는게 Variational AutoEncoder 라고 할 수 있다.
VAE는 어떤 매끄러운 latent space가 먼저 선행된다 가정하고
거기서부터 우리가 복잡한 규칙을 통해서 데이터를 sampling할 수 있다고 생각한다.
일반적인 AutoEncoder들은 이 latent space 에서 mapping 된 어떤 벡터를 바로 찾아내지만
즉 latent space에서 sampling 한 어떤 난수를 바로 찾아내지만
Variational AutoEncoder 의 경우는 이런 latent space를 묘사하는 모수를 직접 추론한다.
encoder 로 부터 나오는 값은 임의의 latent vector 가 아니라 확률분포의 모수이며
이 모수로 부터 sampling 한 난수로 부터 다시 데이터를 복원하는 방법을 사용한다.
그러니까 decoder는 그냥 난수를 받아서 그걸 이미지로 만들어낸다는 소리다.
이게 참 희한하고 희한한 부분이다.

위에서 볼 수 있듯 encoder는 아주 복잡한 data space 를 매끄럽고 다루기 쉬운 prior distribution 으로 mapping 한다.
베이즈 룰 처럼 뒤집어서 생각하자는 것이다.
우리에게 주어진 data space 가 먼저 주어진, 선행하는 것이 아니고
어떤 매끄러운 prior distribution으로부터
약간의 복잡한 규칙을 통해 sampling 된 것이라고 보자는 것이다.
data space에서 data가 sampling 되는 것을 observation 이라고 한다.
그러면 우리는 이 latent space를 공유하는 두개의 확률모델을 연결하여
mapping과 reconstructing이 연쇄적으로 일어나는 모델도 상상할 수 있다.
다만 일반적으로 prior distribution을 잘 찾아내는 작업이 더 힘들다.
왜냐하면 data가 mapping 되는 매끄러운 곡면이 있는지 조차 알고 있지 않기 때문이다.
잘 훈련된 decoder 가 어떤 매끄러운 곡면으로부터 데이터를 잘 복원한다고 가정하고
(또 그런 곡면이 있다고 가정하고)
encoder 의 분포가 매끄러운 latent space에 가장 가깝게 만드는, 그러니까
$p_{\theta}(\bf{z}|\bf{x})$ 와 $q_{\phi}(\bf{z}|\bf{x})$ 가 같아지게 만드는 방법을 사용할 수 있다.
다시말해
$q_{\phi}(\bf{z}|\bf{x})$ : variational distribution of encoder (찾고자 하는 분포)
데이터 x 가 주어지면 $\phi$에의해 모델링된 분포로 부터 z 를 추출할 확률
$p_{\theta}(\bf{z}|\bf{x})$ : true posterior distribution of decoder (추론된 분포)
$\theta$에의해 모델링된 분포로 부터 데이터 x 가 관측되면 그 분포의 given vector가 z 일 확률
이 두 분포가 같아지면 동일한 latent space를 정확히 공유한다고 볼 수 있다.
이 계산을 위해서 Kingma는 본인의 thesis에 이렇게 정리해 두었는데
decoder 의 data space 에 대한 likelihood를 encoder의 확률분포로 풀어서
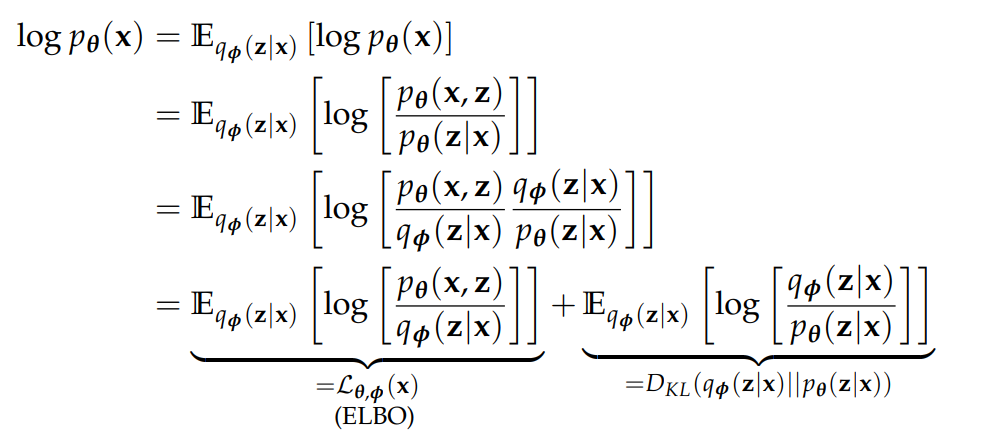
위와 같이 소개했다.
더하기 뒤에 나온 KL-divergence는
우리가 낮추고자 하는 objective function을 정확히 표현하고 있고 항상 0보다 크거나 같음을 증명할 수 있다.
그러므로 encoder의 latent space와 decoder의 latent space가 정확히 일치할때
더하기 왼쪽의 항은 decoder의 data space에대한 likelihood의 lower bound 가 되게 된다.
사실 우리는 decoder를 정의하면서 z의 true posterior distribution을 가정했으므로
측정할 수 있는 값은 ELBO 밖에 없다고 할 수 있다.

이때 ELBO를 최대화 하는 것은
decoder의 data space에대한 likelihood 가 증가하거나
decoder에서 가정한 z의 true posterior와 encoder가 추론하는 approximate posterior간의
KL-divergence 가 감소하는 것을 나타낸다.
그리고 z 에대한 conditional prob.가 아닌 joint prob.로 되어있기 때문에

이렇게 reconstruction term과 encoder 의 approximate posterior 를 강제할 수 있는
prior fitting term을 만들어 내는 것이 가능하다.
그리고 normal distribution은 KL-divergence가 수렴하므로
우리는 normal distribution으로 encoder 의 approximate posterior 강제하여
매끄러운 latent space를 얻어내는 것이 가능하다.
그리고 Adversarial AE는 이 prior fitting term을 adversarial objective function으로 바꿈으로써
이 ELBO를 최대화하는 작업을 한다.
왜 AAE는 더 진보된 모델인가 하면
우리가 KL-divergence를 잘 구해낼 수 있는 분포는 그렇게 많지 않기 때문에
수렴을 보장하기도 사실 힘들다.
하지만 이 부분을 adversarial objective function로 바꾸게 되면 어떤 분포와도 수렴을 보장할 수 있게 되기 때문에
굉장히 다양한 분포로 latent space를 강제할 수 있다.
2) 과제 수행 과정 / 결과물 정리
3) 피어세션 정리
4) 학습 회고
'딥러닝 머신러닝 데이터 분석 > BoostCampAITech' 카테고리의 다른 글
| [ BoostCamp ] Day-17 학습로그( PyTorch의 구조 학습 ) (0) | 2021.08.20 |
|---|---|
| [ BoostCamp ] Day-16 학습로그( Pytorch Basic ) (0) | 2021.08.19 |
| [ BoostCamp ] Day-11 학습로그(RNN) (0) | 2021.08.15 |
| [ Boost Camp ] Day-10 학습로그( CNN ) (0) | 2021.08.13 |
| [ Boost Camp ] Day-9 학습로그 (0) | 2021.08.10 |


댓글