본 문서는 강의의 내용을 토대로 다른 자료들을 공부하고 취합하여 재 해석한 내용으로 강의 내용과 많이 다를 수 있음.
이하 모든 출처가 생략된 자료는 모두 Boost Camp AI Tech의 자료에서 발췌한 것임을 밝힘.
// CNN
우리가 너무나도 잘 알고 있는 CNN.
과연 잘 알고 있는 것이 맞는 건가 싶을 때가 한두번이 아니다.
CNN에 대한 자세한 설명들은 너무나도 많으므로 강의에 나왔던 내용중에
카운터 펀치가 될만한 내용들 위주로 정리를 할까 한다.
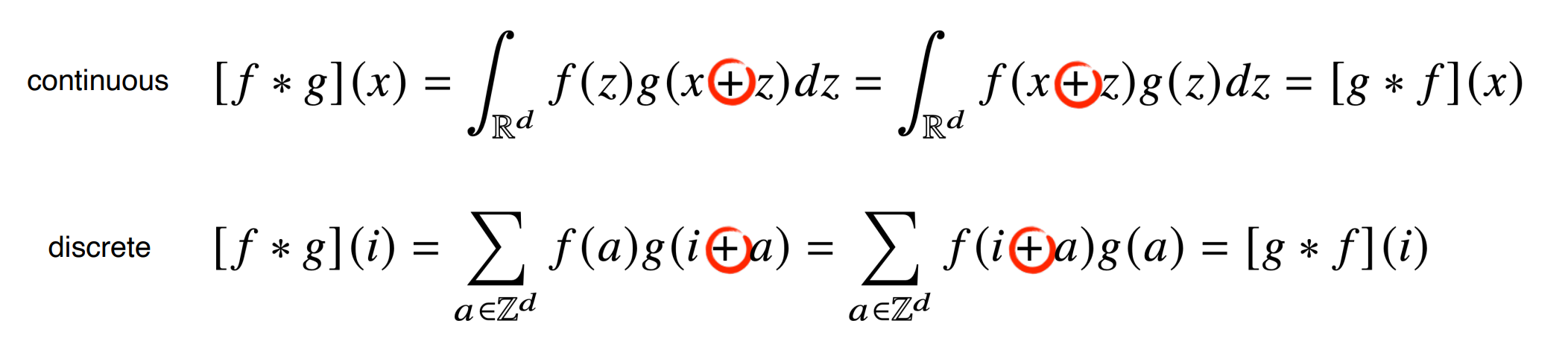
우선은 이 부분.
우리가 convolution이라고 알고 부르는 이 연산은 사실 cross-correlation연산이라고 한다.
사실은 필터가 신호를 스캔할때 신호의 방향과 같은 방향으로 스캔하느냐 혹은 다른 방향으로 스캔하느냐
그런 차이 뿐이지만 기원이나 의미를 보면 확실히 다른 연산이라는 것을 알 수 있다.
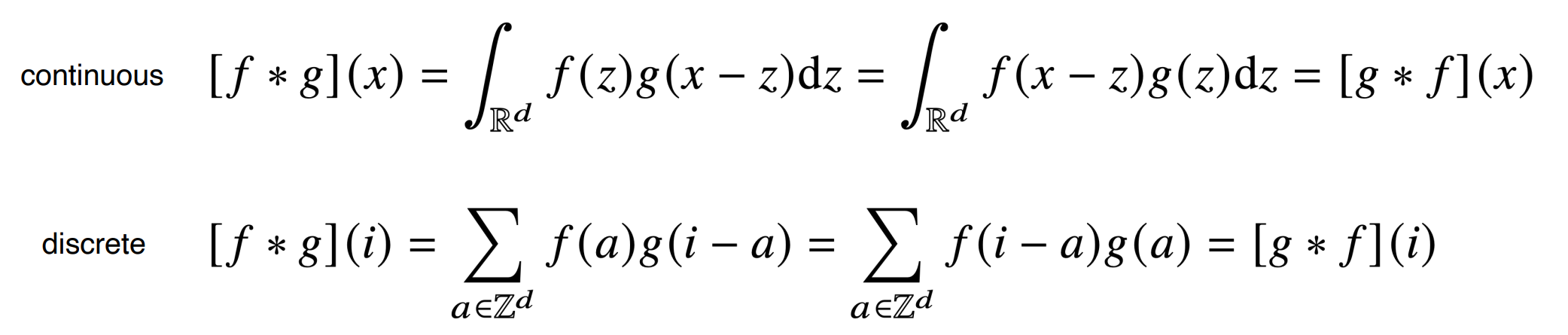
우선은 원래 convolution을 보면 f 와 g 가 곱해져있고 f 의 정의역에 해당하는 부분을 모두 적분하는 것을 알 수 있다.
이것은 f 와 g 가 PDF 혹은 PMF 일때, 그리고 확률 변수 X와 Y가 합이 정해져 있을때
p( X=x, Y=y ) = f(X)*g(Y) 의 joint probability를 나타내기 위해서 사용한다.
X와 Y 가 어떤 방식으로 커플링되어있고 한쪽의 결정이 다른 한쪽의 결정에 영향을 줄때
X와 Y 둘이 동시에 관측될 확률을 말한다.
X + Y = Z 라고 한다면 Y = Z - X 이므로
$$P(Z = z) = \sum_{x{\in}X} p_{X}(x) * p_{Y}(z - x) $$
가 되고 이때 X에 대한 PMF가 f고 Y에 대한 PMF 가 g 라면 아래처럼 바뀐다.
$$P(Z = z) = \sum_{x{\in}X} f(x) * g(z - x) $$
따라서 이런 경우 그러니까 확률론에서 말하는 "진짜" convolution의 경우에는
우리의 직관과 조금 다르게 움직 일 수 있으므로 그럴땐 joint probability로 이해해야한다.
cross-correlation의 경우는 우리의 직관과 일치하는데
보통은 확률론 관점에서 접근하지 않고 signal processing 관점에서 일치한다.
확률론 관점에서는 역시 f 와 g 가 PDM 혹은 PMF 로
하나의 분포를 모수에 따라 이동할때 둘의 확률 분포가 얼마나 유사한지 판단하는 척도가 될 수 있다.
하지만 그런 접근은 이쪽에서는 거의 하지 않고 signal의 filter 개념으로 받아들이는 경우가 대부분이다.
이런 경우 사실은 아래에 링크된 convolution theorem을 알고있을 필요가 있는데
https://en.wikipedia.org/wiki/Convolution_theorem
Convolution theorem - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Theorem that under suitable conditions the Fourier transform of a convolution of two signals is the pointwise product of their Fourier transforms In mathematics, the convolution theore
en.wikipedia.org
일종의 signal에서 filter로 작용하는 convolution filter는 푸리에 도메인 상에서 mask의 역할을 한다.
영상처리도 일종의 signal을 분석하는 것이므로 이러한 관점을 알고있을 필요가 반드시 있다.
여기까지는 강의에 소개된 부분이 아니므로 언급만 하고 넘어가도록 하겠다.
// RNN
RNN은 정말 잘 안다고 말할 수 있는 사람이 얼마나될까 싶은 주제다.
단언코 어렵다.
RNN이전에 여러 sequencial data에 대한 견해들은 Markov chain등의 키워드로 공부하면 된다고 알고있지만
정확한 지식인지는 장담할 수 없다. 나중에 정리해야겠다.
아무튼 강의에서 이야기하는 확률론적 해석은

이전의 모든 데이터가 주어진 경우의 joint probability를 구하는 것이 목적으로
현재 주어진 데이터에 관한 확률은 이전의 모든 데이터가 given된 상태의 conditianal probability를 따르고
베이즈 정리에 의해서 다시 이전 모든 데이터가 관측될 확률의 joint probability와 곱해진 형태를 따른다.
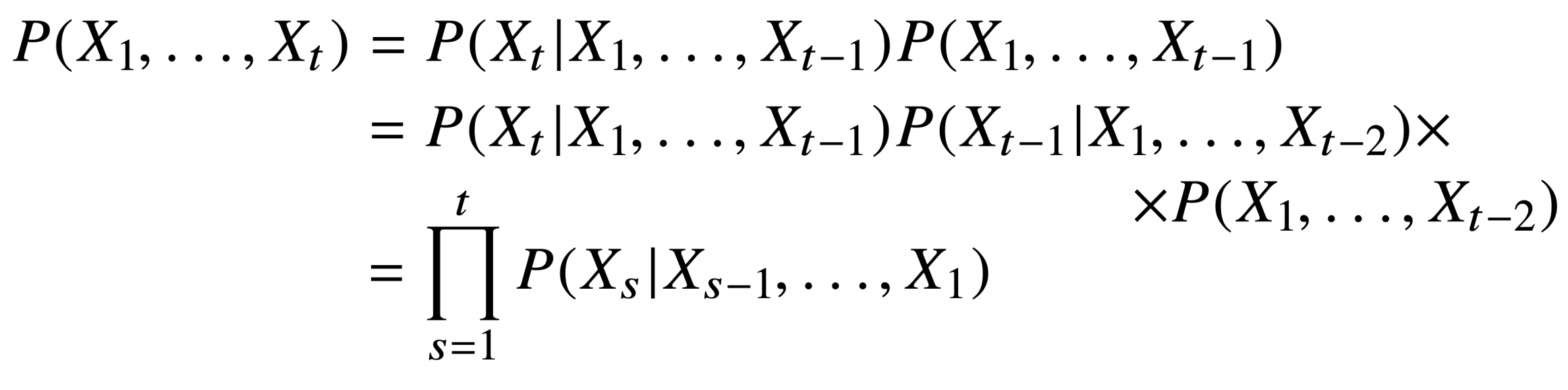
이것은 다시 연쇄적인 작용을 하여서 결국에 위와같은 모양을 가지게 된다.
하지만 일반적인 경우 이전의 모든 데이터가 균등하게 현재의 데이터에 영향을 주는 것이 아니므로
일정 범위 내에서 관측된 데이터를 중점적으로 보는 것이 유리하다.
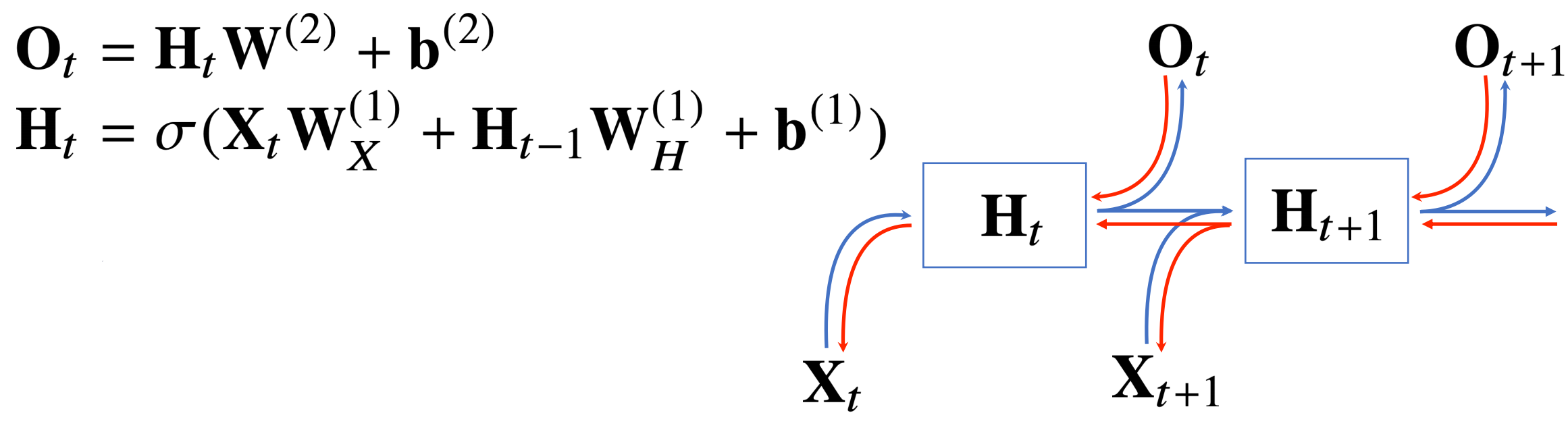
이런식으로 이전에 만들어진 어떤 데이터의 분포가
이후의 데이터 분포를 예측하는데 영향을 주도록 설계된 것이 바로 RNN 이다.
RNN은 이전의 모든 계산이 현재의 계산에 영향을 주고
그러한 과정에서 연산에 들어가는 W가 바뀌지 않기 때문에
Back Propagation Trough Time (BPTT) 라는 독특한 방식으로 역전파가 일어난다.
사실 독특하다기보다는 그냥 연전파를 계산해보면 나오는 것이지만
일반적인 모델들과는 차별점이 있기 때문에 이름을 붙인것 같다.
이 BPTT를 계산해보면 중첩적으로 나타나는 항이 생기는데

저렇게 계속해서 곱해지는 형태의 항이 하나 나오게 된다.
그러면 1보다 클 경우 발산하기 쉽고
1보다 작은 경우 0이 되기 쉽고
음의 값이 나오는 경우 진동하기 쉽다.
따라서 매우 불안정한 항으로 저 항을 일정 구간 끊어서 사용하는 방법이 있는데
이를 truncated BPTT라고 하고 이때 설정해주는 truncated 구간이 적절하지 못한 경우가 많다.
따라서 이를 극복하기 위해서 LSTM이나 GRU 등의 메모리 게이트가 추가된 형식의 모델들이 등장하게 된다.
끝!
'딥러닝 머신러닝 데이터 분석 > BoostCampAITech' 카테고리의 다른 글
| [ Boost Camp ] Day-8 학습로그 (0) | 2021.08.10 |
|---|---|
| [ Boost Camp ] BPTT를 이해해 보자 (4) | 2021.08.09 |
| [ Boost Camp ] Day-2 학습로그( 신경망 학습 ) (0) | 2021.08.06 |
| [ Boost Camp ] Day-1 학습로그 (벡터, 행렬, 선형회귀, SGD) (0) | 2021.08.06 |
| [ BoostCamp ] Day-3 학습 로그 ( 통계학, 베이즈 통계학 ) (0) | 2021.08.05 |




댓글