[ C/C++ ] Int16 에서 float32 로 변환하기 혹은 역변환

//1

일반적으로 실재하는 신호들은 아날로그 신호이다.

아날로그라는 말은 곧 물리학 법칙으로 기술할 수 있는 것들을 말하며

수학적으로는 "적분"으로 기술되는 것들이다.

 

하지만 전자기기에서 이루어지는 거의 모든 신호처리는 샘플링sampling과 양자화quantization에 의해서

띄엄띄엄 점찍어진 이산신호들 즉 디지털 시그널을 기반으로 되어있다.

디지털 신호들은 물리적 법칙보다는 일부 근사와 논리적 가정에 기반한 알고리즘에 의해 기술되고

수학적으로는 "급수"로 기술되는 것들이다.

 

이 아날로그 신호와 디지털 신호사이에 다리역할을 하는 것이 바로

ADC(Analog-to-Digital Converter : 아날로그 -> 디지털)와 DAC(Digital-to-Analog Converter : 디지털 -> 아날로그)이다.

 

ADC는 아날로그 신호를 약속된 규칙으로 샘플링하고 양자화 한 후 이것을 디지털 신호로 반환한다.

DAC는 약속된 샘플링과 양자화 규칙으로 디지털 신호를 읽은 뒤 아날로그 신호로 변환하여 출력한다.

 

양자화 과정을 거칠때 주로 낮은 비트수의 정수형으로 신호의 크기amplitude가 변환되기 때문에

높은 정밀도의 실수형으로 시그널 프로세싱을 하기 위해서는 본문의 과정이 반드시 필요하다.

 

특히 딥러닝의 경우 매우 많은 덧셈과 곱셈이 있기 때문에 자칙 입력값을 큰 수로 집어넣을경우

모델 내부에서 값이 발산하여 학습이 안되는 문제가 있을 수 있다.

 

 

 

 

//샘플링과 양자화

샘플링은 시간축에서 얼마나 자주 점을 찍을 것인가 하는 것으로

중고등학교때 사용하던 시간기록계를 생각하면 편하다.

이미지 출처 : http://study.zum.com/book/12476

다만 저때는 수레의 속력이 얼마나 빠르냐에 따라 점의 간격이 달라졌다면

이번에는 수레는 일정하게 움직이면서 타점을 얼마나 여러번 찍을 것이냐 하는 문제로 보면 된다.

이건 나중에 더 자세하게 다루도록 하겠다.

 

양자화는 반올림을 생각하면 편하다.

만약 이과를 나왔다면 알고있을 가우스기호 혹은 가우스 함수를 생각하면 편하다.

특정한 간격을 미리 나눠놓고 중간에 애매한 값이 들어오면 이 값을 반올림해서

우리가 예측가능한 값으로 만드는 과정이다.

 

샘플링과는 관계없이 이 양자화 과정에서 연속적이던 소리는 낮은 비트수의 정수로 바뀐다.

https://ko.wikipedia.org/wiki/%EC%96%91%EC%9E%90%ED%99%94_(%EC%A0%95%EB%B3%B4_%EC%9D%B4%EB%A1%A0)

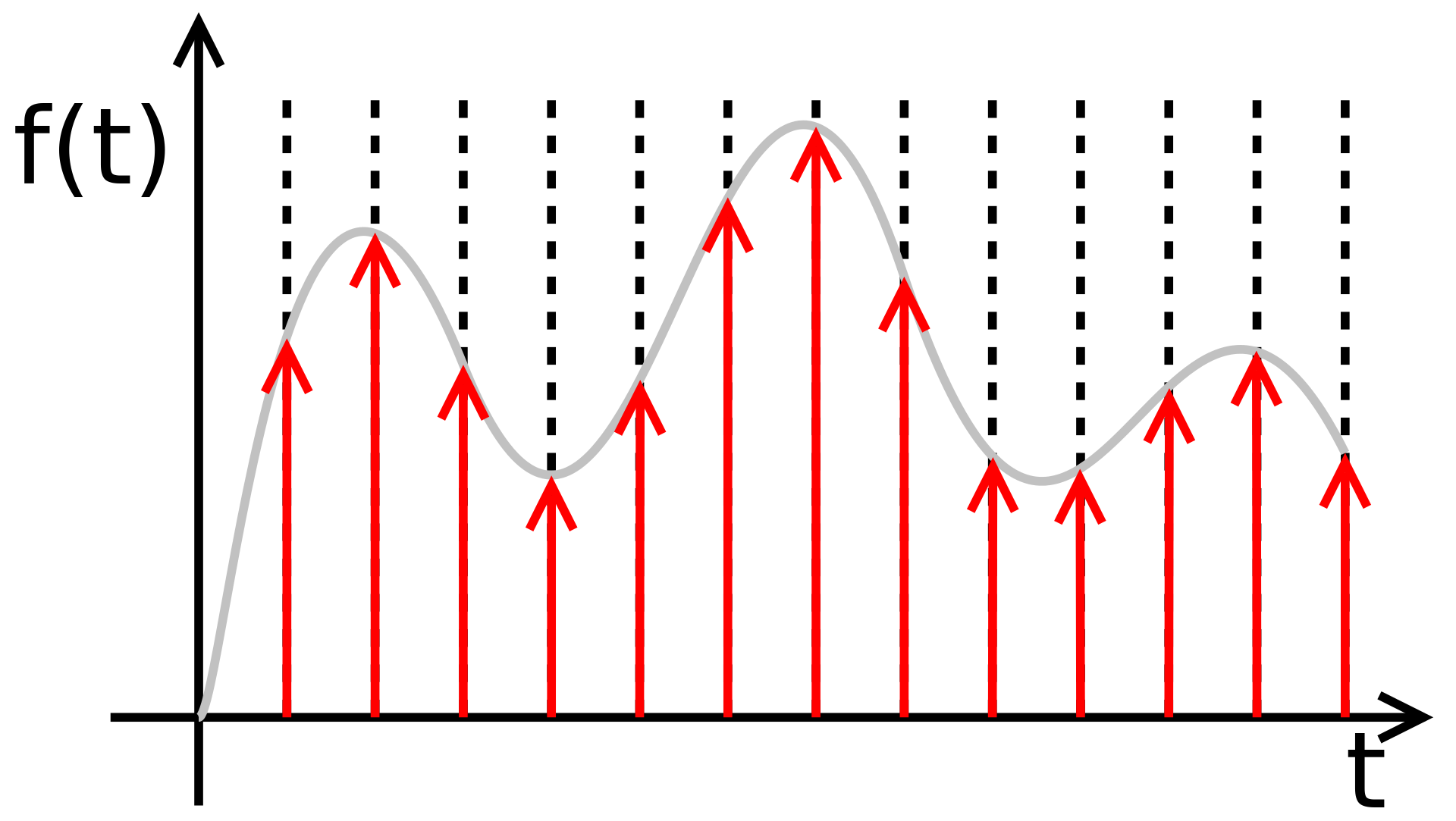
샘플링은 이렇게 시간축으로 디지털화 하기 때문에 신호의 크기(높이)에는 영향을 안주지만

 

https://ko.wikipedia.org/wiki/%EC%96%91%EC%9E%90%ED%99%94_(%EC%A0%95%EB%B3%B4_%EC%9D%B4%EB%A1%A0)

이렇게 양자화의 경우는 그 크기(높이)를 어떤 규칙으로 바꾸기 때문에 문제가 생긴다.

 

특히나 이진수로 표현되는 디지털 신호는 그 크기를 몇 비트로 나누냐에 따라

2의 n제곱 까지 표현되는 정수에 대응시킨다.

따라서 16비트의 경우 양으로는 2^15 -1 까지 그리고 음으로는 -2^15까지 대응시키기 때문에

-32768~32767 (0을 포함하기 때문에 양수는 1 적음) 이라는 굉장히 큰 수로 소리를 표현하게 된다.

 

이러면 급수로 표현되는 수식에서는 굉장히 숫자가 커지게 되고 다루기 어려운 부분이 생긴다.

 

따라서 대체로 -1~1로 표현되는 실수형으로의 변환을 거친 후 다시 -32768~32767로 바꾸는 과정을 거친다.

즉

이런 일련의 과정으로 시그널프로세싱이 진행된다.

사실 ADC나 DAC는 직접적인 하드웨어를 의미하는 것으로 소리에 관한 칩을 설계할때 들어가는 부품이다.

따라서 더 자세한 것은 PCM(Pulse-Code Modulation)을 키워드로 찾아보기 바란다.

 

파이썬이나 일부 고급언어에서는 이 float32를 바로 .wav로 저장하는 것을 지원하지만

저급언어인 C/C++에서는 아주 얄짤없다.

 

나는 분명 잘 처리했는데 너무 큰소리가 찢어질 만큼 난다던가 아무소리가 안나는 경우 이 부분을 점검해야 한다.

 

 

 

 

//Int자료를 float으로 변환하기

 

주의할 점은 두 가지다.

이 두가지만 주의하면 24비트로 소리를 받았건 32비트로 받았건 모두 상황에 맞게 처리할 수 있다.

 

여기서부터는 Signed Int 16bit 을 기준으로 이야기 하겠다.

첫째, Int16의 경우 위와 아래가 비대칭으로 1의 차이가 난다.

둘째, 최고가 1이고 최소가 -1인 값안에 맵핑해야한다.

 

뭐 1과 -1 사이에 넣는건 그냥 최대나 최소로 나누어주는 방식을 쉽게 떠올릴 수 있지만

문제는 내가 가진 데이터의 range max와 range min이 다르다는 것이다.

뭘 겨우 1 차이 나는 걸로 그럼 ㅋㅋ 이라고 할 수 있겠지만 정신머리부터 글러먹은 생각이니

인류를 위해서 연구자의 길은 포기하기 바란다.

 

결론부터 말하자면 아래의 과정으로 올바르게 변환할 수 있다.

 

1. -2^15 ~ 2^15 -1 의 범위를 가지는 데이터에 2^15를 더한다 : [0 ~ 2^16 -1]

2. 1의 결과에 2^16 -1을 나눈다 : [0 ~ 1.0]

※이때 float으로 형변환이 일어나므로 주의해서 나누어준다. davi06000.tistory.com/17 참고

[ C/C++ 삽질 ] C 혹은 C++에서의 나누기 ("/")

3. 2의 결과에 2.0을 곱한다 : [0 ~ 2.0]

4. 3의 결과에 1.0을 뺀다 : [-1.0 ~ 1.0]

 

이 과정을 그림으로 그리면 다음과 같다.

나도 항상 이 과정을 그림으로 머리속에 넣어두고 그때 그때 코드를 짠다.

 

취향에 따라 음의 실수 영역에서 -2.0 까지 만든 후 1을 더해줘도 상관없다.

rangeMAX 에서 rangeMIN까지 정확하게 시그널이 보내지기만 하면 그만이다.

 

이렇게 형변환을 정확하게 하는 방법을 이해하면 어떤 형의 데이터를 받더라도

원하는 범위의 높은 정밀도를 가진 형으로 바꿔서 연산이 가능하다.

 

코드는 아래와 같다.

#include <math.h>

void int16tof32(int* x, float* y, int dataLength)
{
    double t;
    int j;
    for (j = 0; j < dataLength; j++) {
        t = x[j] + pow(2.0, 15.0);    //[ 0, 2^16 -1]
        t = t / (pow(2.0, 16.0) - 1); //[ 0, 1]
        t = 2.0 * t - 1.0;            //[-1, 1]

        *y = (float)t;
        y++;
    }
}

pow()를 사용하기위해서 math.h를 꼭 include 해주자. C++의 경우는 pow에 해당하는 다른 함수를 사용해 주면 된다.

 

역변환은 위의 순서를 역으로 진행하면 된다.

 

1을 더하고

2를 나누고

2^16 -1을 곱하고

2^15를 뺀다

형을 int로 바꿔준다

 

이것만 잘 숙지하면 시그널프로세싱 알고리즘을 짜기도 전에

소리부터 받기위해서 애써야하는 시간을 많이 단축시킬 수 있다.